Newsletter 2021.4 Index
Theme : "The Conference of Fluid Engineering Division (April issue)”
|
Backflow of Liquid Crystal and Development of Microactuators Driven by Backflow Effect
|
Abstract
Although it is well known that the application of a velocity gradient makes liquid crystal molecules rotate and reorient to a different direction, its reverse phenomenon, such that the rotation of the molecules (by applying, for example, an electric field) induces a velocity gradient, is not clearly understood. Since this phenomenon corresponds to the energy conversion from electrical to kinetic energies, to utilize such induced flow leads to development of microactuators(1). Some studies(2)(3) were made for the generation of a flow, which was called “backflow”; however, in these studies, the mechanical applications of the backflow were not considered, although its effect on molecular orientation was investigated.
As a fundamental study for liquid crystal actuators, we prepared a sandwich cell with a movable upper plate (Fig. 1) and used backflow induced by applying repetitively a rectangular wave voltage to drive the upper plate in its plane. We used 4-cyano-4’-pentyl biphenyl (5CB), a low-molar mass nematic liquid crystal. The speed of the plate depends significantly on the frequency of the applied voltage as shown in Fig. 2; the speed increases with increasing frequency, attaining a maximum value of 120 μm/s at 175 Hz. Further increases in frequency, however, produce a gradual decrease in plate speed because the molecules of the liquid crystal respond too slowly to the change in voltage at the higher frequencies(4). To predict the driving performance of liquid crystal actuator, we proposed a simple one-dimensional model that combines the motion of the upper plate of the liquid crystal cell with the flow of the liquid crystal(5). As shown in Fig. 2, the proposed model qualitatively predicted the motion of the upper plate.
Because of the fluidity of liquid crystals, there is no restriction on the shape of the objects to be driven. Hence, if the object has a round shape, then the induced shear force produces a rotational motion of the object. Figure 3 shows a liquid crystal micromotor that exploits the backflow effect. The motor is composed of concentric glass cylinders, the gap being filled with 5CB. As shown in Fig. 4, the maximum speed of rotation obtained was approximately 30 rpm for a pulsed voltage of 10 V, duty ratio of 5%, and frequency of 500 Hz(6).
Key words
Liquid Crystal, Complex Fluid, Backflow, Actuator
Figures
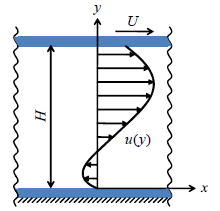
Fig. 1 Schematic of a sandwich cell and coordinate system.
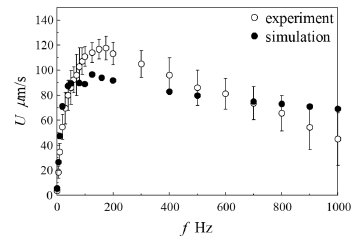
Fig. 2 Dependence of the speed of the upper plate on frequency of the applied voltage when V=10 V, D=5 %, and H=10 μm. The speed exhibits a sharp increase, attains a maximum value of 120 μm/s at f=175 Hz, and then decreases gradually with increasing f.
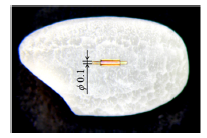
Fig. 3 Microscope image of a liquid crystal motor placed on a grain of rice for a comparison of scale. The outer diameters of the inner and outer cylinders are 0.1mm and 0.2mm, and the gap between two cylinders is 5μm.
Fig. 4 Video of rotation of the inner cylinder. The maximum rotation speed is 30rpm when V=10V, f=500Hz and D=5%.



