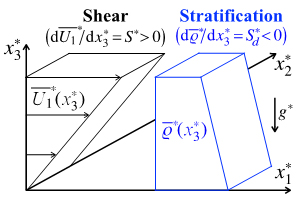
Figure 1 Sketch of the mean field.
流れの読み物
― 特集テーマ:流体工学部門講演会 3月号 ―
| リンク一覧にもどる | |
|
日本機械学会第98期流体工学部門講演会において,光栄にも若手優秀講演フェロー賞を頂きました.この場をお借りして,選考委員会並びに流体工学部門の皆様に御礼を申し上げます.本報では,講演内容である,成層せん断乱流の直接数値シミュレーションと線形過程について紹介させて頂きます.
鉛直上方ほど密度の小さい成層流体は,大気・海洋などの地球環境だけでなく,液化天然ガスタンクや原子力プラントといった大型施設内にしばしば現れ,流体運動に大きな影響を及ぼす.成層流体の平均流速は通常,不均一と言ってよく,局所的には水平せん断流が形成される傾向にある.よって,成層流体におけるせん断効果の解析は非常に重要であり,成層せん断乱流における熱や物質の輸送メカニズムに関する研究は,これまで数多くなされてきた.
成層せん断乱流の数値計算としては,これまで,Gerz & Schumann(1)や Jacobitz et al.(2)によるDNSがある.また,理論的な研究として,Hanazaki & Hunt(3)は,Rapid Distortion Theory(RDT)を用いて,成層やせん断が乱流場に与える影響を解析的に求めた.RDTは,支配方程式中の線形項である浮力項や平均せん断項が大きく,非線形効果が相対的に小さい場合に,線形化した近似方程式を解くものである.線形化のおかげで,しばしば解析解を得ることができ,成層やせん断が乱流に与える基本的な効果を知るのに役立つ.例えば,先行研究(3)では,(せん断の強さが一定の条件下で)成層の強さを変化させて数値計算(1)との比較を行っている.しかし逆に,(成層の強さが一定の条件下で)平均せん断の効果を解析した数値計算はなく,せん断効果が成層流体に及ぼす影響は十分に解明されていない.また,RDTが適用できる時間・空間スケールについても十分に調べられていない.本研究では,特にRDTの適用可能な空間スケールを定量的に検証すると同時に,平均せん断の効果をDNSによって解析する.
図1のように,密度の鉛直勾配(S*d = const. < 0, * は次元量)と,平均水平速度の鉛直勾配(S* = const. > 0)を持つ成層せん断流を考える.等方的な速度撹乱を初期条件として与え,密度撹乱は初期には与えない.速度撹乱u*i ,圧力撹乱p*,密度撹乱ρ*を支配する無次元の基礎方程式は,(1)〜(3)に示した連続の式,Boussinesq近似を施した運動方程式,密度撹乱の輸送方程式となる.
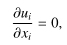 |
(1) |
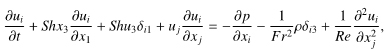 |
(2) |
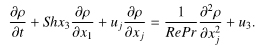 |
(3) |
ここで,各方程式は,初期積分長L*0,初期rms速度U*0,代表密度-L*0S*dを用いて無次元化されている.系の挙動を決定する無次元パラメタは,初期Reynolds数Re=U*0L*0/ν*,Prandtl数Pr=ν*/κ*,初期Froude数Fr=U*0/(N*L*0),初期せん断Sh=S*L*0/U*0である(N*∝|S*d|1/2:浮力振動数,ν*:動粘性係数,κ*:密度の拡散係数).本研究では,Re=50,Pr=1と固定し,Fr(逆数が成層の強さ)とSh(せん断の強さ)を変化させる(表1参照).式(1)〜(3)を,周期境界条件を課した一辺L(=L*/L*0)の立方体を計算領域として,スペクトル法を用いた直接数値計算により解く.成層せん断乱流で形成される大スケールの空間構造を解像するため,計算領域の一辺は初期積分長の15〜20倍に設定する.格子点数は20483とし,時間発展には3次精度のRunge-Kutta法を用いる.

Case |
Sh | Fr | L (DNS) |
Sh1Fr1 |
1 | 1 | 30π |
Sh1Fr01 |
1 | 0.1 | 30π |
Sh10Fr1 |
10 | 1 | 30π |
Sh10Fr01 |
10 | 0.1 | 40π |
Sh15Fr01 |
15 | 0.1 | 40π |
Sh20Fr01 |
20 | 0.1 | 40π |
Sh30Fr01 |
30 | 0.1 | 40π |
RDTでは,成層やせん断の線形効果が強く,非線形効果が相対的に十分弱い状況を仮定して,支配方程式を線形化する.式(2),(3)の非線形項を無視した上で,実空間上の撹乱量をスペクトル分解することで得られるRDT方程式は,Pr = 1の場合については,解析解が得られている(3).支配方程式(2),(3)の各項の大きさを渦の大きさl*とその特性速度u*(l*)で評価すると,非線形項が線形項に対して無視できるのは,時間スケールで表すとl*/u*(l*)>>1/N*,かつl*/u*(l*)>>1/S*を満たす場合となる.つまり,スケールl*の渦がせん断や成層によって急速に変化する場合にRDTが適用できる.これらの条件を,運動エネルギー散逸率ε*~u*(l*)3/l*を用いて,長さスケールに関する条件に書き直すとl*>>l*O,かつl*>>l*Cとなる.ここでl*O=(ε*/N*3)1/2,はOzmidovスケール,l*C=(ε*/S*3)1/2はCorrsinスケールであり,それぞれ,成層あるいはせん断の効果が及ぶ最小スケールを表す.本研究では,上記の不等式を満たす長さスケールでRDTが適用できるか否かを確かめるべく,DNSとRDTの比較を行った.
まず,成層とせん断による流れ構造の典型的な時間変化を見るため,図2に,表1のSh1Fr1の場合について,運動エネルギーとポテンシャルエネルギーの空間分布(DNS)の時間変化を示す.初期(図2a並びに図2d, t =2)に等方的であった速度撹乱や密度撹乱は,時間と共に鉛直(x3)方向に扁平,かつ,主流(x1)方向に細長く伸びた大スケール構造を形成する.これは,成層による流体の鉛直変位の抑制と,せん断による引き延ばし効果によるものである.なお、Pr=1であるため,速度撹乱と密度撹乱の空間スケールはほぼ同じである.
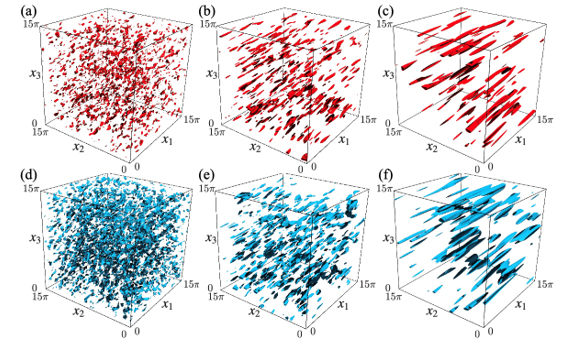
Figure 2 Distribution of the kinetic energy ui2/2 (red) and the potential energy ρ2/(2Fr2)(blue) obtained by DNS (Case Sh1Fr1). (a,d) t=U*0t*/L*0=2, (b,e) t = 10 and (c,f) t = 20.
次に,DNSとRDTの結果を比較する.図3は,Sh1Fr1のt =1, 4, 8における運動エネルギースペクトルとポテンシャルエネルギースペクトルをDNSとRDTにより計算した結果である.時刻t = 1, 4(図3 a,b)では,kO (=lO-1)とkC (=lC-1)よりも低波数側でDNS(実線)とRDT(破線)のスペクトルがよく一致する.その後,時刻t = 8(図3 c)では,エネルギーが少ない波数域(Kolmogorov波数よりも高波数側(k > kK))でDNSとRDTのスペクトルに若干の差が見られるが,エネルギーが時間的に増加する低波数側(k < 0.5)ではRDTが良い近似を示す.これは,図2に示した大スケール構造の形成がRDTによって予測できることを示す結果である.
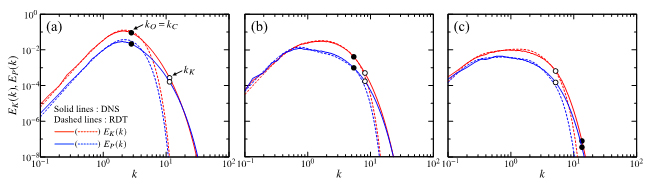
Figure 3 DNS and RDT results of the kinetic-energy spectrum EK(k) and the potential-energy spectrum EP(k) at (a) t=1 , (b) t=4 and (c) t=8 for Sh1Fr1. The symbol ● on the solid lines (DNS) indicates the Ozmidov wavenumber kO=lO-1 which is equal to the Corrsin wavenumber( kC=lC-1 ), and ○ indicates Kolmogorov wavenumber kK=lK-1 (l*K=(ν*3/ε*)1/4: Kolmogorov scale).
図4は,Sh1Fr1に比べて成層(Fr)やせん断(Sh)の強さを変更したケースについて,図3と同様にDNSとRDTのスペクトルを求めた結果である.時刻は全てt = 1.5である.Sh1Fr1に比べ成層のみを強くしたSh1Fr01(図4a)では,k < kC (< kO) の低波数域でDNSとRDTのスペクトルがよく一致している.Sh1Fr1に比べてせん断のみを強くしたSh10Fr1(図4b)では,k < kO(< kC)でDNSとRDTが一致する.Sh1Fr1と比べて成層とせん断の両方を強くしたSh10Fr01(図4c)では,成層とせん断の両方の効果がKolmogorovスケール以下まで達しており,エネルギーを持つ全てのスケールでDNSとRDTのスペクトルが一致している.以上より,OzmidovスケールとCorrsinスケールのどちらよりも大きいスケール(k < kOかつk < kCの低波数域)に対してRDTが適用できることがわかった.
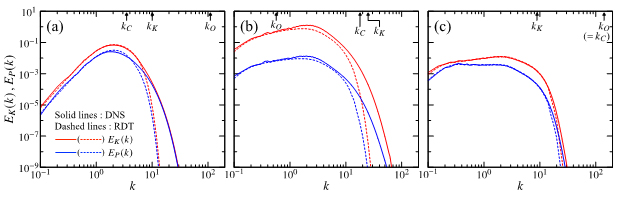
Figure 4 DNS and RDT results of the kinetic-energy spectrum EK(k) and the potential-energy spectrum EP(k) at t=1.5 for (a) Sh1Fr01, (b) Sh10Fr1 and (c) Sh10Fr01. The arrows at the top of each figure indicate the Ozmidov, Corrsin and Kolmogorov wavenumbers.
最後に,線形効果が支配的なスケール( lO, lCより大スケール)において,せん断効果が密度成層乱流にもたらす影響をDNSにより解析した.図5に,Frを0.1に固定してShを10(赤線)から30(黒線)まで増加させた場合の運動エネルギースペクトルEK(k),ポテンシャルエネルギースペクトルEP(k),及び鉛直運動エネルギー(u32/2)のスペクトルE33(k)を示す.図5に示した時刻(t =1)ではkK<kO(≤kC)であり,成層とせん断の効果はKolmogorovスケールにまで及んでいるが,このとき図5(a, b)より,せん断効果が強くなると,運動エネルギーとポテンシャルエネルギーの低波数成分が増加することがわかる.一方,鉛直運動エネルギースペクトルE33(k)(図5c)を見ると,せん断が強いほど低波数成分が増加するものの,高波数成分は減少する.こうしたE33(k)のSh依存性はHanazaki & Hunt(3)のRDTによる結果と定性的に一致している.
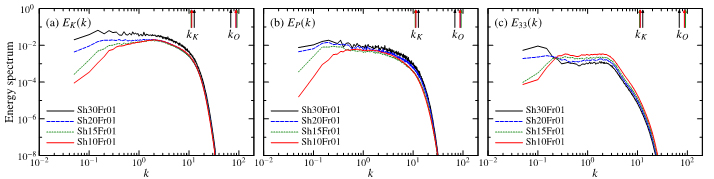
Figure 5 Shear-parameter dependence of the energy spectra (a)EK(k), (b)EP(k) and (c)E33(k) at t=1 obtained by DNS. The arrows at the top of each figure show the four Kolmogorov wavenumbers and four Ozmidov wavenumbers corresponding to the four simulated cases. The Corrsin wavenumber satisfies kC ≥ kO (kC = Sh3/2Fr3/2kO) in all the figures.
成層せん断乱流について直接数値計算(DNS)を行い,線形理論(RDT)が適用可能な空間スケールを検討すると同時に,この乱流の特性を調べた.その結果,成層・せん断効果の及ぶ最小スケールであるOzmidovスケール及びCorrsinスケールよりも大きいスケールに対し,RDTによる近似が適用できることがわかった.また,平均せん断は,大スケールではエネルギーの増加に寄与し,小スケールでは鉛直運動エネルギーを減少させることがわかったが,この性質もRDT(3)による結果と一致した.
本研究はJSPS科研費18K13685の助成を受けたものである.また,本研究の成果はHPCIシステム利用研究課題(課題ID: hp200020) ならびに平成31年度,令和2年度地球シミュレータ公募課題として海洋研究開発機構の地球シミュレータを用いて得られたものである.