Newsletter  2014.1  Index

Theme : "The Conference of Fluid Engineering Division" Preface M.Oshima, Y. Takahashi, H. Yoshikawa Development of coaxial electromagnetic energy conversion device for efficient wind energy utilization Akira TANIDA, Hidemasa TAKANA (Tohoku University) Augmentation and attenuation of large-scale intermittent structures in rotating channel flow Takahiro ISHIDA (Tokyo University of Science) An attempt to measure wall shear stress fluctuation in a turbulent wall jet Takuya SAWADA, Osamu TERASHIMA, Yasuhiko SAKAI, Kouji NAGATA, Mitsuhiro SHIKIDA, Yasumasa ITO (Nagoya University) Concentration statistics near the turbulent / non-turbulent interface of a planar liquid jet with a chemical reaction Takahiro NAITO, Tomoaki WATANABE, Yasuhiko SAKAI, Kouji NAGATA, Yasumasa ITO, Osamu TERASHIMA (Nagoya University) The valuable experience of the Dreams of Flow Contest Tsubasa OZAKI, Jumpei OHKUBO, Hiroaki KOBAYASHI, Kodai FUJITA (Hokkaido University) A story of creation for Dreams of Flow Contest Kodai FUJITA, Hiroaki KOBAYASHI (Hokkaido University)   |  Back  |

 

Augmentation and attenuation of large-scale intermittent structures in rotating channel flow

Takahiro ISHIDA Tokyo University of Science

Abstract

In the transitional channel flow, the large-scale intermittent structure of localized turbulence, which is called turbulent stripe, can be found in the form of stripe arrangement. The structure of the turbulent stripe is laminar-turbulent banded pattern being oblique with respect to the streamwise direction (Re_τ = u_τδ/ν = 64 and Ro_τ = 2Ωδ/u_τ = 0.02 in Fig. 1, u_τ: the friction velocity, δ: half the channel width, Ω: system angular velocity). We performed the direct numerical simulation at the transitional Reynolds numbers and very low-rotation numbers, with focusing on the turbulent stripe in the plane Poiseuille flow subjected to spanwise system rotation.

Rotating plane Poiseuille flow is known to consist of a suction side and a pressure side. On the suction side of the channel, where the system rotation has the same direction with the vorticity of the mean shear, the flow becomes stable. Even for turbulent states, the stable stratification of the half channel would attenuate turbulent motions in this region. On the pressure side, the flow becomes unstable due to the Coriolis-force instability, and the longitudinal roll cells may occur as an initial stage of laminar-turbulent transition and survive even with turbulent background at high Reynolds numbers. We captured the turbulent stripe in rotating channel flows (Fig. 1).

Fig. 2 shows each component of the velocity fluctuations u’_i (u_i = U_i + u’_i, U_i:mean velocity, u’_i:velocity fluctuation) in rotating plane Poiseuille flow. It is obviously observed in (a) of the figures that streamwise streaky structures are not evenly distributed and seems to form bands or clusters. The intermittent stripe pattern can be determined in Fig. 2(b). As for the spanwise velocity fluctuation, somewhat coherent structures are clearly seen to emerge around the turbulent regions, as shown in Fig. 2(c). In common with the streamwise component, either positive or negative fluctuation of spanwise component dominantly appears in the upstream area of the turbulent region, while w’ with the opposite sign dominates the downstream area. This phenomenon is the spanwise secondary flow of interest.

The spanwise mean velocity and the skewness factor of the spanwise velocity fluctuation are given in Fig. 3. Although their averaged values should become zero in the turbulent channel flow, they have significant magnitudes in the flow state accompanied by turbulent stripe because of the spanwise secondary flow along the turbulent bands. It is interesting to note that, at very low rotation number, they are significantly increased compared with those in static system. At high rotation numbers, the peak value of the spanwise velocity component decreases. This reduction is caused by the development of the longitudinal roll cells due to a strong rotation.

We found the augmentation and diminution of the features that characterizes the turbulent stripe in the spanwise-rotating channel flow. The turbulent stripe is slightly enhanced by a weak Coriolis instability: that is, the magnitude of the spanwise velocity component is intensified. The occurrence of turbulent stripe is important from the viewpoint of mass and heat transport in the spanwise direction because the spanwise velocity component has a distinguished value. It would be impossible in the featureless turbulence or the laminar flow, since the mean spanwise velocity component is zero. The system rotation even with very low rotation number gives rise to non-zero mean spanwise velocity. It is favorable to the engineering application because of efficient transfer by turbulent stripe.

 

Key words

Large-scale turbulent structure, Rotating flow, Transition

 

Figures

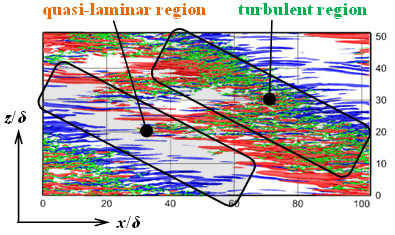
Fig. 1  Visualization of instantaneous flow field at Reτ (= u_τδ/ν) = 64 and Ro_τ (= 2Ωδ/u_τ) = 0.02, in an (x, z)-plane. Red isosurface,u’⁺ > 3.5, blue, u’⁺ < –3.5, green, II’⁺ = u’_i,ju’_j,i < –0.015 (which is equivalent to the vortical position). The mean flow moves from left to right. The super script + and * indicate the quantities normalized by wall unit and the outer scale.

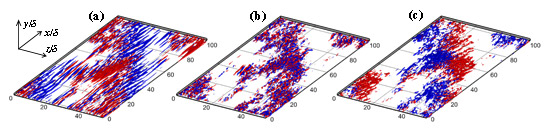
Fig. 2  Visualization of instantaneous flow field at Re_τ= 64 and Ro_τ= 0.015. (a) Red isosurface, u’⁺ > 3.5; blue, u’⁺ < -3.5, (b) Red isosurface, v’⁺ > 0.75; blue, v’⁺ < -0.75, (c) Red isosurface,w’⁺ > 1.5; blue, w’⁺ < -1,5. The mean flow move from left below to upper right.

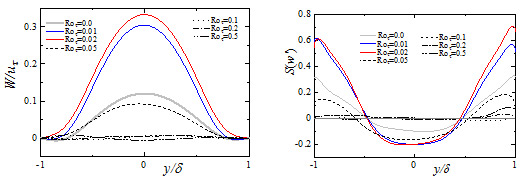
Fig. 3  Spanwise mean velocity profile and skewness factor of w’ at Re_τ = 64
for various rotation number.